Breadth and Depth Oriented (MN)

The following algorithm (MN-Algorithm) combines the MNB- and MND-Algorithms:

1. For each argument column , create a list where is the longest prefix of column without variables
2. If then use the first clause as a separate partition (without indexing) else
   • sort the in descending order (w.r.t. their length) into the list
   • := length of first element in
   • := position of last column in with length with (this means that in order to enlarge the index tree breadth the partition size may be reduced, e.g. by at most 30%);
     := length of this column;
     first elements of ;
     reorder w.r.t. selectivity
   • create a partition consisting of the first clauses; index the argument columns in ( index tree breadth)
   • for each constant/functor occurring multiply in one argument column of this partition do
     • form a procedure containing all selected clauses and the remaining argument columns in (only columns to the right of the current one)
     • apply the MN-Algorithm recursively to this procedure ( index tree depth)
3. If any clauses are left go to 1 else stop

MN-Algorithm applied to norm example:

1. • 
   • use clause 1 as first partition
2. • 
   • 
   • 
   • 
   • ( is too short, thus index tree breadth )
   • 
   • second partition consists of clauses 2 - 9, indexing takes place on first argument
   • and/2 occurs four times in indexing column:
     • form procedure from selected clauses:

       

     • applying MN-Algorithm to this procedure:

       

   • or/2 occurs four times in indexing column; result analogously to and/2:

     

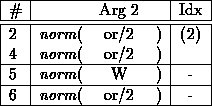
Resulting index tree: