Next: Using Arguments Other Up: Extensions of the Previous: Quadratic Indexing

Our Approach

The next sections will describe our approach. Instead of directly presenting our final indexing technique, its components are introduced in order of increasing complexity.

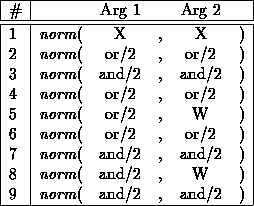
The following part of a PROLOG program (a normalizer producing DNFs of propositional formulas) is used to demonstrate our heuristics for generating index trees: 



norm(X, X) :- literal(X).
norm(or(X, Y), or(X, Y)) :- literal(X), literal(Y).
norm(and(X, Y), and(X, Y)) :- literal(X), literal(Y).

norm(or(X, Y), or(X1, Y)) :-
        literal(Y),
        norm(X, X1).

norm(or(X, or(Y, Z)), W) :-
        norm(or(or(X, Y), Z), W).

norm(or(X, and(Y1, Y2)), or(X1, Y12)) :-
        norm(X, X1),
        norm(and(Y1, Y2), Y12).

norm(and(X, Y), and(X1, Y)) :-
        literal(Y),
        norm(X, X1).

norm(and(X, and(Y, Z)), W) :-
        norm(and(and(X, Y), Z), W).

norm(and(X, or(Y1, Y2)), and(X1, Y12)) :-
        norm(X, X1),
        norm(or(Y1, Y2), Y12).

Only the following information (entirely extracted from the clause heads) is used for the index tree generation; all algorithms in this paper can easily be extended to use additional information such as inner structure arguments and ``guards'' (see section 12.1):

The following sections describe the heuristics for our indexing techniques:

Michael Sintek - sintek@dfki.uni-kl.de